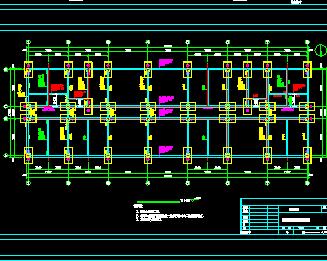
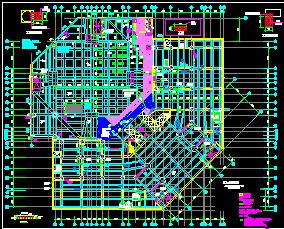
���ކ�Ԫ����50�����Դ�ں��չ����w�C(j��)�Y(ji��)��(g��u)�ľ�ꇷ������Y(ji��)��(g��u)��ꇷ����J(r��n)����һ��(g��)�Y(ji��)��(g��u)���Կ����������ނ�(g��)���W(xu��)С��Ԫ��B�Ӷ��ɵļ����w��������Ԫ���W(xu��)���ԵĄ��Ⱦ�ꇿɱ����������еĴu�ߡ��b����һ������ṩ����(g��)�Y(ji��)��(g��u)�����W(xu��)������
��(y��ng)������Ԫ������B�m(x��)�w�r(sh��)�������^(q��)��֞����ނ�(g��)��Ԫ������ÿ��(g��)��Ԫ��ָ�����ނ�(g��)��(ji��)�c(di��n)��һ������J(r��n)��������Ԫ�ڹ�(ji��)�c(di��n)�B�ӳ�һ�M��Ԫ�ļ����w������ģ�M��ƽ����^(q��)���M(j��n)�з�����ͬ�r(sh��)�x����(ch��ng)����(sh��)�Ĺ�(ji��)�c(di��n)ֵ������ȡ��(ji��)�c(di��n)λ���������δ֪�������O(sh��)һ��(g��)��ֵ����(sh��)���Ƶر�ʾλ�Ʒֲ�Ҏ(gu��)����������׃��ԭ������������������Ԫ��(ji��)�c(di��n)����λ��֮�g�����W(xu��)�����P(gu��n)ϵ���õ�һ�M�Թ�(ji��)�c(di��n)λ�ƞ�δ֪���Ĵ���(sh��)���̽M���Ķ���⹝(ji��)�c(di��n)λ�Ʒ�����